La técnica más básica para calcular integrales de una variable real se basa en el teorema fundamental del cálculo. Se procede de la siguiente forma:
- Se escoge una función f(x) y un intervalo [a, b].
- Se halla una antiderivada de f, es decir, una función F tal que F' = f.
- Se emplea el teorema fundamental del cálculo, suponiendo que ni el integrando ni la integral tienen singularidades en el camino de integración,
- Por tanto, el valor de la integral es F(b) − F(a).
Nótese que la integral no es realmente la antiderivada, sino que el teorema fundamental permite emplear las antiderivadas para evaluar las integrales definidas.
A menudo, el paso difícil de este proceso es el de encontrar una primitiva de f. En raras ocasiones es posible echar un vistazo a una función y escribir directamente su primitiva. Muy a menudo, es necesario emplear una de las muchas técnicas que se han desarrollado para evaluar integrales. La mayoría de ellas transforman una integral en otra que se espera que sea más manejable. Entre estas técnicas destacan:
- Integración por cambio de variable
- Integración por partes
- Integración por sustitución trigonométrica
- Integración de fracciones parciales
Incluso si estas técnicas fallan, aún puede ser posible evaluar una integral dada. La siguiente técnica más común es el cálculo del residuo, mientras que la serie de Taylor a veces se puede usar para hallar la primitiva de las integrales no elementales en lo que se conoce como el método de integración por series. También hay muchas formas menos habituales para calcular integrales definidas; por ejemplo, se puede emplear la identidad de Parseval para transformar una integral sobre una región rectangular en una suma infinita. En algunas ocasiones, se puede evaluar una integral empleando un truco; un ejemplo de este tipo se puede ver en la integral de Gauss.
Los cálculos de volúmenes de sólidos de revolución se pueden hacer normalmente con la integración por discos o la integración por capas.
Los resultados específicos que se han encontrado empleando las diferentes técnicas se recogen en la tabla de integrales.
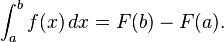
No hay comentarios:
Publicar un comentario